トマト充填問題(2)

 トマトを二次元的に箱に詰める問題は、Circle Packing in squareという問題に一般化できそうだ。理論はともかく、結果だけ使わせていただく。

スーパーで売っている箱は16x18cmだが、面倒なのでここでは17x17cmの正方形と仮定する。

まず、箱に詰める個数nを決める。→Circle Packing in squareから最大の充填半径を見る→楕円球仮定で重さを計算→前回の補正(1.32x-14)を使ってトマト形状での重さに変換。

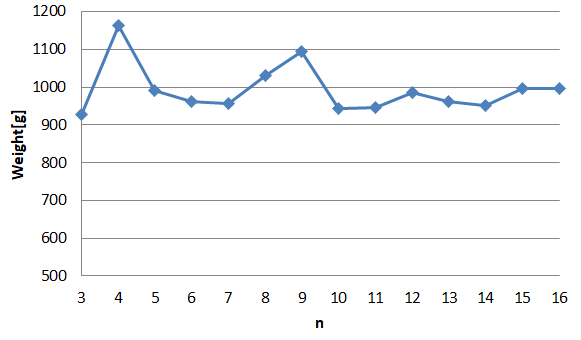
これを見ると、4, 9が特異的にオトクなのがわかる。8も悪くない。配置から考えると16もよいはずだが、ここまでくると全体の個数が多いからかそこまででもない。

実際には、9個配置(3x3)で直径56mm。高さは56mm平均なので、これ以上小さい場合はトマト形状モデル範囲外となる

実際に購入してみた。箱いっぱいに詰められた5個と7個。7個の方がトマトの隙間が少なく見え、量があるように見えるが、実測してみると5個の方がオトクだ。上記のグラフの予想でも5個入りの方が30gほどオトク。同程度オトクなのが確認できた。

つまり、箱に密に詰まっている場合、4 → 9 →8 →5...の順に選べばよいことになる。店頭でも選択は容易だ。